Q1. A surface consists of charges +q, −3q and +5q. There is a charge +4q
outside the surface. What is the flux over the surface?
Solution
The flux over a surface is given from Gauss’ law as
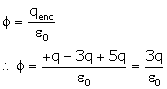
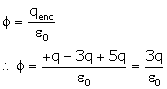
Q2. Electric flux through a surface does not depend on
Solution
Electric flux through a surface is
 Hence, from the above expression, we see that the flux depends on the
field, surface area and angle ϴ.
Hence, from the above expression, we see that the flux depends on the
field, surface area and angle ϴ.
Q3. What is the magnitude of the electric field at a field point 3 m from a point charge q = 6 nC?
Solution
Given:


Q4. The force constant K depends on
Solution
In Coulomb’s law, the force constant K is
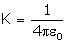 Hence, K depends only on ε0, the
permittivity of the medium. So, K depends only on the nature of the medium.
Hence, K depends only on ε0, the
permittivity of the medium. So, K depends only on the nature of the medium.
Q5. If  , calculate the electric flux through a surface of area 20 units in Y-Z Plane.
, calculate the electric flux through a surface of area 20 units in Y-Z Plane.
 , calculate the electric flux through a surface of area 20 units in Y-Z Plane.
, calculate the electric flux through a surface of area 20 units in Y-Z Plane.Solution
Area vector  in Y-Z plane points along outward along positive x-direction is,
in Y-Z plane points along outward along positive x-direction is,
 =
= 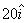 . Hence the flux is:
. Hence the flux is:
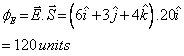
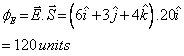
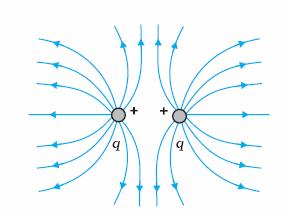
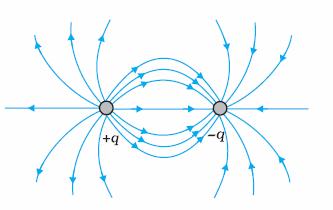
Q6. Sketch the electric lines of force for two equal positive point charges.
Solution
The field lines around a system of two equal positive charges (q, q) shows mutual repulsion between two charges.

Q7. Two
identically charged particles are separated by a distance of 4 Å.
What is the magnitude of charge on each if the Coulomb repulsive force on
each of them is 5.1 × 10−9 N?
Solution
The Coulomb force between two charged particles is
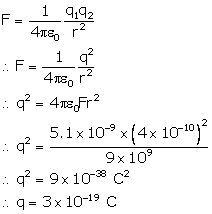
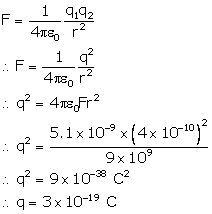
Q8. What will be the coulomb force between two charges, when the distance between them is reduced to half?
Solution
According to coulomb's law  [where r is the distance between two charges]
when the distance between them is reduced to half then force become,
[where r is the distance between two charges]
when the distance between them is reduced to half then force become,
 Hence, the force between charges is increased by 4 times.
Hence, the force between charges is increased by 4 times.
 [where r is the distance between two charges]
when the distance between them is reduced to half then force become,
[where r is the distance between two charges]
when the distance between them is reduced to half then force become,
 Hence, the force between charges is increased by 4 times.
Hence, the force between charges is increased by 4 times.
Q9. ‘A force on any charge due to a number of other charges is the vector
sum of all the forces on that charge due to other charges’ is the statement
of
Solution
According to the principle of superposition, a force on any charge due
to a number of other charges is the vector sum of all the forces on that
charge due to other charges.
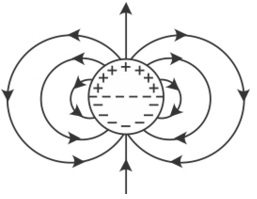
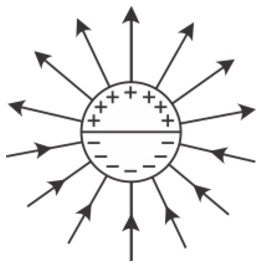
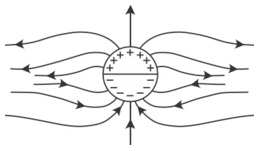
Q10. A long cylindrical shell carries positive surface charge σ in the upper half and negative surface charge - σ in the lower half. The electric field lines around the cylinder will look like figure given in:
Solution
We can consider the shell to be a dipole. So, at the equatorial points the electric lines should be downwards. Also, the field lines should start from the positive terminal and end at the negative terminal. The electric field lines should be smooth and continuous. Figure (1) satisfies all the required conditions.

Q11. A hollow conducting sphere of radius 10 cm is given a charge of 20 μC. What is the electric field intensity? a. At the centre of the sphere, and b. On the outer surface of the sphere?
Solution
Here Q=20 μC = 20 × 10-6 C
R = 10 cm = 0.10 m
a. Electric Field at the centre of the sphere is zero, because intensity at any point inside a hollow sphere is always zero.
b. Electric Field on the outer surface of the sphere is-
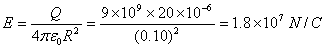
Q12. Why does the person sitting in a car is saved from atmospheric lightning?
Solution
On lightning, the charge resides on the surface of car due to shielding effect. There is no charge inside the car .Hence electric field is zero, and the person is saved.
Q13. The dipole moment of a system consisting of a proton and an electron
separated by 4 nm is
Solution
The magnitude of the charge on a proton and an electron is the same (q
= 1.6 × 10−19 C).
Hence, the dipole moment of the system is


Q14. The expression q = ne signifies which property of electric charge.
Solution
According to quantisation of charge, the charge is always an integral multiple of the standard value e. So, q = ne is the term associated with quantisation of charge.
Q15. Electric flux through a surface is maximum when
Solution
Electric flux through a surface is
 Hence, from the above expression, we see that the flux is maximum when
cosϴ is maximum, i.e.
when ϴ = 0°.
Hence, from the above expression, we see that the flux is maximum when
cosϴ is maximum, i.e.
when ϴ = 0°.
Q16. What is the direction of dipole moment?
Solution
The direction of dipole moment is from negative to positive charge.
Q17. Two charges +10 μC and -10 μC are held 2 cm apart. Calculate the electric field at a point on the equatorial line at a distance of 50 cm from the centre of the dipole.
Solution
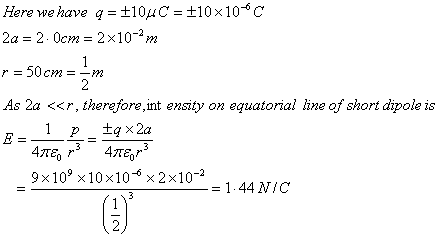
Q18. Two point charges q1 and q2, of magnitude 20 nC and –20 nC respectively, are placed 0.2 m apart. Calculate the electric field at points A, B and C.
Solution
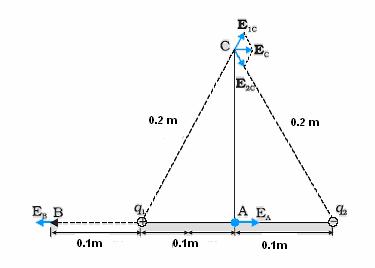 The electric field vector E1A at A due to the positive charge q1 points towards the right and has magnitude
The electric field vector E1A at A due to the positive charge q1 points towards the right and has magnitude
Q19. Which of the following has a permanent dipole moment?
Solution
A polar molecule has charges whose centres do not coincide with each
other. Therefore, they have a dipole moment even in the absence of an
external electric field. This dipole moment is permanent.
Non-polar molecules develop a dipole moment only in the presence of an
electric field. When the field is removed, the dipole moment is lost.
Q20. Two similar and equally charged metal spheres A and B repel each other with a force of 3 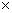 10-6 N. A third identical uncharged sphere C is touched with A and then placed at the mid point between A and B. calculate the net electric force on C.
10-6 N. A third identical uncharged sphere C is touched with A and then placed at the mid point between A and B. calculate the net electric force on C.
Solution
Force between A and B is: Here, F = 12 N
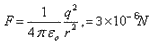 On touching C with A, charge on A as well as C will be q/2. Now the net force on C is:
FC = FCB - FCA
On touching C with A, charge on A as well as C will be q/2. Now the net force on C is:
FC = FCB - FCA

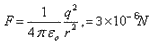 On touching C with A, charge on A as well as C will be q/2. Now the net force on C is:
FC = FCB - FCA
On touching C with A, charge on A as well as C will be q/2. Now the net force on C is:
FC = FCB - FCA

Q21. Two point charges 3 μC and + 7μC repel each other with a force of 12 N. If each is given an additional charge -5 μC, what will be the new force between them?
Solution
Q22. What are the factors on which the torque on a dipole depends?
Solution
The torque on a dipole is
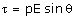 Hence, the torque depends on
Dipole moment p, which in turn depends on the charge and the distance of separation of the two charges
Electric field intensity E
Angle ϴ between the dipole moment and the electric field
Hence, the torque depends on
Dipole moment p, which in turn depends on the charge and the distance of separation of the two charges
Electric field intensity E
Angle ϴ between the dipole moment and the electric field
Q23. State
some properties of field lines.
Solution
Properties of electric field lines:
a. Field
lines start from the positive charge and end at the negative charge.
b. If
there is a single charge, then the field lines may start or end at infinity.
c. Field
lines form continuous curves without any breaks in a charge-free region.
d. Two
field lines can never intersect each other.
e. Field
lines do not form closed loops.
Q24. A
square surface of side 10 cm is placed inside a uniform electric field of 10
N/C. The normal to the surface makes an angle of 60°
with the field direction. What is the flux through the surface?
Solution
The electric flux through an area element is


Q25. Sketch the electric lines of force two equal and opposite point charges placed near each other.
Solution
The field lines around a system of two equal and opposite charges (q, -q) shows mutual attraction between two charges.

Q26. Explain the principle of a device that can build up high voltages of the order of few million volts.
Draw a schematic diagram and explain the working of this device.
Is there any restriction the upper limit of the high voltages set up in this machine? Explain.
OR
(a) Define electric flux. Write its S.I units.
(b) Using Gauss's law prove that electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
(c) How is the field directed if (i) the sheet is positively charged, (ii) negatively charged ?
Solution
Van de graaf generator is the machine that can build up high voltages upto a few million volts and is used to accelerate charged particles to high energies.
Working principle:
Consider a large spherical conducting shell of radius R with uniform charge density and total charge Q.
Then, the potential
 If a sphere of radius r0 (r0 < R) carrying total charge q is placed at the center of the larger sphere, potential due to inner sphere is
If a sphere of radius r0 (r0 < R) carrying total charge q is placed at the center of the larger sphere, potential due to inner sphere is
 Therefor, total potential is ø(r) = øq (r) + øQ (r) and
Therefor, total potential is ø(r) = øq (r) + øQ (r) and
 Therefore for positive q, whatever Q is, the small sphere is at a higher potential then the shell.
Therefor, if an electric contact is made between the inner sphere and other shell, charge would flow from the small sphere to the shell. By repeating the process, a large amount of charge can be piled up the shells with consequent high potential and field. This is the principle behind the working of van de graaf generator.
Therefore for positive q, whatever Q is, the small sphere is at a higher potential then the shell.
Therefor, if an electric contact is made between the inner sphere and other shell, charge would flow from the small sphere to the shell. By repeating the process, a large amount of charge can be piled up the shells with consequent high potential and field. This is the principle behind the working of van de graaf generator.
 Fig. Schematic diagram of a van de Graaaf generator
Working:
Practically, an insulating column support a large spherical conducting shell with radius of a few metres. There are two pulleys, one at the center of the shell and the other at the ground. A long narrow belt made of insulating material passes over the pulleys, Charge is sprayed on the belt at the lower pulley by means of a discharge through a metallic brush (with sharp points) connected to a high voltage surface. The belt is moved rapidly by a motor driving the lower pulley. The positive charge thus transferred continuously upward is removed from the, again by a metallic brush connected to the shell. In this way, the shell builds up a huge voltage.
The machine can generate high-energy beams in the range of 10 MeV or so. The highest voltage that this device can build up voltages till they match with the break down voltages of the surrounding air.
OR
(a) Electric flux Δø through a Surface of area ΔS is defined as the scalar product of the electric field
Fig. Schematic diagram of a van de Graaaf generator
Working:
Practically, an insulating column support a large spherical conducting shell with radius of a few metres. There are two pulleys, one at the center of the shell and the other at the ground. A long narrow belt made of insulating material passes over the pulleys, Charge is sprayed on the belt at the lower pulley by means of a discharge through a metallic brush (with sharp points) connected to a high voltage surface. The belt is moved rapidly by a motor driving the lower pulley. The positive charge thus transferred continuously upward is removed from the, again by a metallic brush connected to the shell. In this way, the shell builds up a huge voltage.
The machine can generate high-energy beams in the range of 10 MeV or so. The highest voltage that this device can build up voltages till they match with the break down voltages of the surrounding air.
OR
(a) Electric flux Δø through a Surface of area ΔS is defined as the scalar product of the electric field  and the area vector Δ
and the area vector Δ .
Δø =
.
Δø =  . Δ
. Δ = EΔS cosθ
where θ is the angle between the directions of
= EΔS cosθ
where θ is the angle between the directions of  and Δ
and Δ . The magnitude of the area vector Δ
. The magnitude of the area vector Δ is the same as the area, whereas its direction is along the outer normal to the surface.
SI unit of electric flux is NC-1m2.
(b) Electric field due infinite sheet of charge:
Consider a large plane sheet of charge with charge density σ Cm-2 The electric field lines will emanate normally from this surface.
We want to determine the electric field at a point distant r from this surface.
Gaussian surface
is the same as the area, whereas its direction is along the outer normal to the surface.
SI unit of electric flux is NC-1m2.
(b) Electric field due infinite sheet of charge:
Consider a large plane sheet of charge with charge density σ Cm-2 The electric field lines will emanate normally from this surface.
We want to determine the electric field at a point distant r from this surface.
Gaussian surface
 To apply Gauss's Law Let us consider two circular planes, each of area A, equidistant from and on either sides of the sheet of charge.
Let us join these two surface to construct a cylinder, as show Once again, there are three surfaces. The curved surface of no consequence because no filed lines pass through it. For each of the circular surfaces,
To apply Gauss's Law Let us consider two circular planes, each of area A, equidistant from and on either sides of the sheet of charge.
Let us join these two surface to construct a cylinder, as show Once again, there are three surfaces. The curved surface of no consequence because no filed lines pass through it. For each of the circular surfaces,  is in the same direction as that of the outward normal.
Thus,
is in the same direction as that of the outward normal.
Thus, 
 But, the net charge enclose inside the cylinder is given by |q| = |σ| x A
hence,
But, the net charge enclose inside the cylinder is given by |q| = |σ| x A
hence,  Vectorially, we write
Vectorially, we write  is the unit vector in the direction of the outward normal to the sheet of change.
(c) If sheet is (i) positively charged, field will be outward from the sheet and (ii) if the sheet is negative charged then the field will be in wards, ie directing towards the sheet.
is the unit vector in the direction of the outward normal to the sheet of change.
(c) If sheet is (i) positively charged, field will be outward from the sheet and (ii) if the sheet is negative charged then the field will be in wards, ie directing towards the sheet.
 If a sphere of radius r0 (r0 < R) carrying total charge q is placed at the center of the larger sphere, potential due to inner sphere is
If a sphere of radius r0 (r0 < R) carrying total charge q is placed at the center of the larger sphere, potential due to inner sphere is
 Therefor, total potential is ø(r) = øq (r) + øQ (r) and
Therefor, total potential is ø(r) = øq (r) + øQ (r) and
 Therefore for positive q, whatever Q is, the small sphere is at a higher potential then the shell.
Therefor, if an electric contact is made between the inner sphere and other shell, charge would flow from the small sphere to the shell. By repeating the process, a large amount of charge can be piled up the shells with consequent high potential and field. This is the principle behind the working of van de graaf generator.
Therefore for positive q, whatever Q is, the small sphere is at a higher potential then the shell.
Therefor, if an electric contact is made between the inner sphere and other shell, charge would flow from the small sphere to the shell. By repeating the process, a large amount of charge can be piled up the shells with consequent high potential and field. This is the principle behind the working of van de graaf generator.
 and the area vector Δ
and the area vector Δ .
Δø =
.
Δø =  . Δ
. Δ = EΔS cosθ
where θ is the angle between the directions of
= EΔS cosθ
where θ is the angle between the directions of  and Δ
and Δ . The magnitude of the area vector Δ
. The magnitude of the area vector Δ is the same as the area, whereas its direction is along the outer normal to the surface.
SI unit of electric flux is NC-1m2.
(b) Electric field due infinite sheet of charge:
Consider a large plane sheet of charge with charge density σ Cm-2 The electric field lines will emanate normally from this surface.
We want to determine the electric field at a point distant r from this surface.
Gaussian surface
is the same as the area, whereas its direction is along the outer normal to the surface.
SI unit of electric flux is NC-1m2.
(b) Electric field due infinite sheet of charge:
Consider a large plane sheet of charge with charge density σ Cm-2 The electric field lines will emanate normally from this surface.
We want to determine the electric field at a point distant r from this surface.
Gaussian surface
 is in the same direction as that of the outward normal.
Thus,
is in the same direction as that of the outward normal.
Thus, 
 But, the net charge enclose inside the cylinder is given by |q| = |σ| x A
hence,
But, the net charge enclose inside the cylinder is given by |q| = |σ| x A
hence,  Vectorially, we write
Vectorially, we write  is the unit vector in the direction of the outward normal to the sheet of change.
(c) If sheet is (i) positively charged, field will be outward from the sheet and (ii) if the sheet is negative charged then the field will be in wards, ie directing towards the sheet.
is the unit vector in the direction of the outward normal to the sheet of change.
(c) If sheet is (i) positively charged, field will be outward from the sheet and (ii) if the sheet is negative charged then the field will be in wards, ie directing towards the sheet.
Q27. What is the cause of electrification when one body is rubbed with another body?
Solution
The cause of electrification is the transfer of electrons from one body to another.
Body losing electrons acquires positive charge and the body receiving electrons acquires an equal amount of negative charge.
Q28. Draw the electric lines of force for: (a) Equal and same point charges (b) Equal and opposite point charges
Solution
(a) Electric lines of force for equal and same point charges.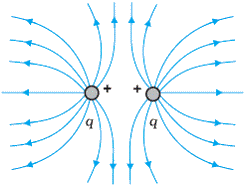 (b) Electric lines of force for equal and opposite point charges.
(b) Electric lines of force for equal and opposite point charges.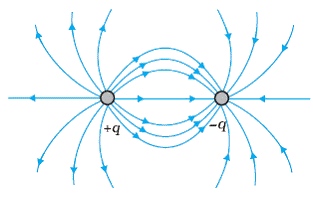
 (b) Electric lines of force for equal and opposite point charges.
(b) Electric lines of force for equal and opposite point charges.
Q29. What will be the net resultant force when the electric dipole moment  is parallel to non uniform electric field
is parallel to non uniform electric field  ?
?
 is parallel to non uniform electric field
is parallel to non uniform electric field  ?
?Solution
In this case there will also be a net force on the dipole since the positive and negative charges will feel different forces F = qE due to the different external field E at the location of charges +q and –q.
In the example shown the dipole and hence its dipole moment is aligned parallel to the external increasing field.
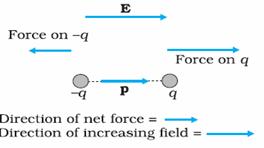 The force on positive charge F = qE exceeds the force on negative charge since the positive charge is in a stronger field.
The net resultant force is directed parallel to the direction of electric field.
The force on positive charge F = qE exceeds the force on negative charge since the positive charge is in a stronger field.
The net resultant force is directed parallel to the direction of electric field.
 The force on positive charge F = qE exceeds the force on negative charge since the positive charge is in a stronger field.
The net resultant force is directed parallel to the direction of electric field.
The force on positive charge F = qE exceeds the force on negative charge since the positive charge is in a stronger field.
The net resultant force is directed parallel to the direction of electric field.
Q30. Two point charges of +2 × 10-19 C and +8 × 10-19 C are separated by a distance of 2 metre. Find the point on the line joining them at which the electric field is zero. 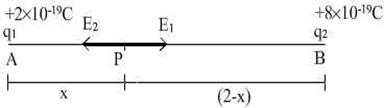

Solution
Let P be the point at distance x from A, where the electric field is zero.
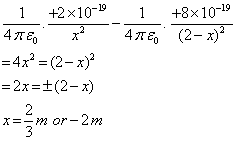 At x = -2 is not possible, because electric field due to both charges will be in same direction. So x = -2 m is not a possible solution.
Hence electric field is zero at 2/3 m to the right of charge q1.
At x = -2 is not possible, because electric field due to both charges will be in same direction. So x = -2 m is not a possible solution.
Hence electric field is zero at 2/3 m to the right of charge q1.
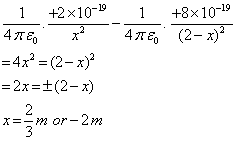 At x = -2 is not possible, because electric field due to both charges will be in same direction. So x = -2 m is not a possible solution.
Hence electric field is zero at 2/3 m to the right of charge q1.
At x = -2 is not possible, because electric field due to both charges will be in same direction. So x = -2 m is not a possible solution.
Hence electric field is zero at 2/3 m to the right of charge q1.
Q31. What would happen if the same charge is passed through the conducting rod of a gold leaf electroscope?
Solution
Gold leafs of electroscope move away from each other. It happens because the body with the same charge repels each other.
Q32. Explain why a glass rod held in hand can be charged by rubbing with flannel but a copper rod cannot be charged like this.
Solution
A glass rod is insulating. The charge appears on it due to rubbing and stay on it. However a copper rod is good conductor. Any charge developed on it flows to earth through our body. So copper rod cannot be charged like this. It can be charged by providing it a plastic or rubber handle.


Comments
Post a Comment