10

Q1. Why does light appear to travel in a straight line in spite of its wave nature?

Solution

When a portion of a wave is obstructed by an obstacle or aperture, diffraction occurs, which depends upon the size of the obstacle or aperture which in turn is related to the wavelength of the wave. If the aperture or obstacle is large compared with the wavelength, the bending of waves is not noticeable and the wave propagates in the straight line. Since the wavelength of light (4000 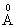 to 8000 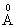) is very small as compared with the size of ordinary object and apertures, diffraction of light is not easily noticeable and hence light appears to travel in a straight line.  

Q2. Discuss the condition for sustained interference

Solution

In order to produce a stable interference, the following conditions should be satisfied:- The two sources must be coherent. The waves that are interfering must have approximately the same amplitude, otherwise the resultant            interference pattern will lack contrast. The Light must be monochromatic. Otherwise, the fringes of different colours will overlap. The two sources must be close to each other. This will enable a large fringe width. The two sources must be narrow. The two sources should emit waves continuously.  

Q3. In Young's double slit experiment, the source gives out white light. One slit is covered with the red filter and the other one with the blue filter. Discuss about the nature of interference.

Solution

As the light from the two sources is of different wavelength (colours), therefore the two sources are no longer coherent. Hence, no stable interference pattern will be obtained and there will be uniform illumination.

Q4. When a tiny circular obstacle is placed in the path of the light of a distant source, a bright spot is seen at the center of the shadow of the obstacle. Explain why?

Solution

Waves diffracted from the edge of the circular obstacle interfere constructively at the center of the shadow of circular obstacle. As a result, a bright spot is seen at the center of the shadow of the obstacle.   

Q5. In Young's double slit experiment, the distance between the slit is kept smaller than the wavelength of the light. What is the effect?

Solution

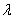Fringe width, .If d< ,then 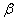>D. That is the fringe width becomes very large and even a single fringe may occupy the entire screen. In such case, Interference will not be seen.  

Q6. In a Young's double slit experiment, the slits are 0.2 mm apart and the screen is 1.5 cm away.It is observed that the distance between the central bright fringe and fourth dark fringe is 1.8 cm.Find the wavelength of light used.

Solution

Q7. Distinguish between inference and diffraction of light.

Solution

 No Interference Diffraction 1 It arises due to superposition of two wave fronts coming from the coherent sources. It is produced due to the superposition of secondary wavelets originating from the different parts of the same wavefront. 2 All bright fringes are of the same intensity. All bright fringes are not of the same intensity.They are of varying intensity. 3 The width of the interference fringes are usually equal. Diffraction fringes are never of the same width.

Q8. An analyzing nicol examines two adjacent plane polarized beams A and B whose planes of polarization are mutually perpendicular .In one position of the analyzer, beam B shows zero intensity. From this position a rotation of 30⁰ shows the two beams are matched (i.e. of equal intensity).Find the intensity ratio of the two beams.

Solution

The intensity of the transmitted light is given by 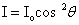.Initially, the beam B shows zero intensity. This means that for beam B .As the planes of polarization of the two adjacent plane polarized beams A and B are mutually perpendicular, it is clear that 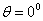for beam A. When the analyzer is rotated through 30^0, 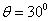for beam A; 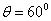for beam B.If  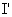is the intensity of beam A, then it will also be that for beam B.  

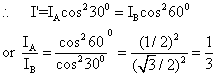
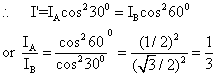
Q9. In a Young's double slit experiment, the interval between the slits is 0.200 mm.For the light of wavelength 6000 A⁰, interference fringes are formed on a screen at a distance of 0.800 m. a) what is the distance of second dark fringe from the central fringe? b) What is the distance of second bright fringe from the central fringe?

Solution

Q10. Two Polaroid’s are used to study polarization. If the analyzer is rotated through the angles of 45⁰, 90⁰   and 180⁰  in turn, how much the intensity of light coming out of the analyzer be affected by these angles of rotation, as compared to the initial intensity?

Solution

Let the intensity of light coming out of polarizer be I_0. If the analyzer subtends an angle 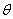 with the polarizer axis, then the intensity of transmitted light will be I=I₀cos²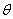. Now if 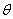=45⁰, then  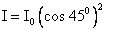= 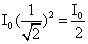If 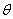= 90⁰, then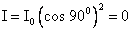.  (i.e complete darkness) And if 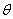= 180⁰, then 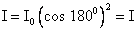₀(-1)²=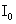. (Maximum)

Q11. Does the law of conservation of energy holds good for diffraction?

Solution

The law of conservation of energy holds good for the phenomenon of wave diffraction. Due to diffraction we obtain maxima and minima intensities at different points. From points of minimum intensity the energy has been shifted to the points of maximum intensity. Thus, there is a re distribution of energy but the total energy remains conserved.  

Q12. Why does sky appears blue?

Solution

The scattering of light by a molecule is inversely proportional to the fourth power of wavelength of light . Thus the sky appears blue because the scattered light has a large mixture of shorter wavelength light (violet and blue) than of longer wavelength light (Yellow and red).

Q13. Light of wavelength 5500 passes through a single slit of width 0.01 m. Find the angular diffraction to the first dark band of the diffraction pattern.

Solution

The angular diffraction to the first dark band of the diffraction pattern is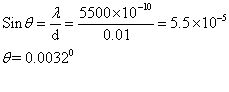

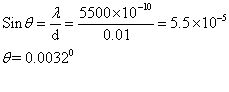
Q14. The refractive index of the denser media is 1.732. Calculate (i) the polarizing angle of medium,(ii)the angle of refraction.

Solution

Here n=1.732   (i)According to Bewsters law,  tan i_p=n    Therefore polarizing angle i_p=tan^-1 n                                            =tan^-1(1.732)                                            =60⁰    (ii) At the polarising angle, the reflected and the refracted ray are perpendicular to each other.       Therefore angle of refraction r = 90⁰ - i_p                                                  =90⁰ - 60⁰                                                  =30⁰

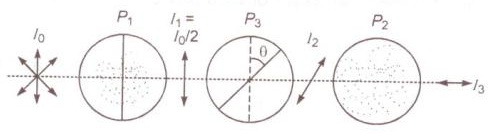
Q15. Two polaroids are set in crossed positions. A third polaroid is placed between the two making an angle  with the pass axis of the first polaroid. Write the expression of the intensity of light transmitted from the second polaroid. In what orientation will the transmitted intensity be (i) minimum and (ii) maximum?

Solution

Q16. If the angle between the pass axes of a polariser and analyser is 45º. Write the ratio of the intensities of original light and the transmitted light after passing through the analyser.

Solution