Q1. In the following fig, the values of capacitances are – 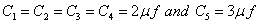 . Calculate the equivalent capacitances between the points P and Q.
. Calculate the equivalent capacitances between the points P and Q. 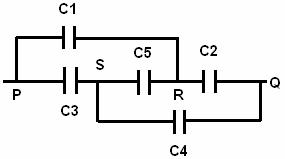

Solution
The given circuit can be redrawn as
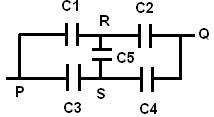
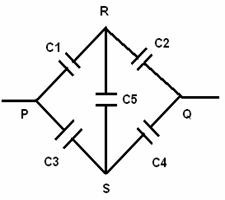 It has been clear that capacitors form wheatstone bridge arrangement.
As
It has been clear that capacitors form wheatstone bridge arrangement.
As 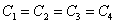
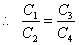 ,
hence, bridge is balanced. (The point R and S are at the same potential)
As no charge can accumulate on C5, which thus become ineffective.
Between P and Q two series combinations (C1C2) and (C3C4) are connected in parallel. If C’ and C’’ are the equivalent capacitances of these combinations then,
,
hence, bridge is balanced. (The point R and S are at the same potential)
As no charge can accumulate on C5, which thus become ineffective.
Between P and Q two series combinations (C1C2) and (C3C4) are connected in parallel. If C’ and C’’ are the equivalent capacitances of these combinations then,
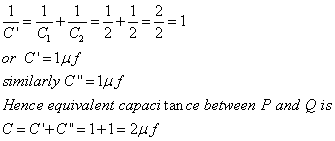

 It has been clear that capacitors form wheatstone bridge arrangement.
As
It has been clear that capacitors form wheatstone bridge arrangement.
As 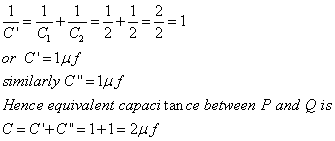
Q2. In the given circuit, charge Q2 on the 2μF capacitor changes as C is varied from 1μF to 3μF. Q2 as a function of 'C’ is given properly by:
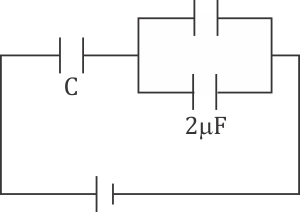 (figures are drawn schematically and are not to scale)
(figures are drawn schematically and are not to scale)
 (figures are drawn schematically and are not to scale)
(figures are drawn schematically and are not to scale)
Solution
 The net capacitance of the circuit is:
The net capacitance of the circuit is:
 Hence, from the above equation, we can say that as C increases, Q2 also increases.
Now, the shape of the curve will be decided by the second derivative of Q2 with C.
Hence, from the above equation, we can say that as C increases, Q2 also increases.
Now, the shape of the curve will be decided by the second derivative of Q2 with C.
 Hence, the correct option will be option (2).
Hence, the correct option will be option (2).
Q3. Why does the electric field inside a dielectric decrease when it is placed in an external electric field?
Solution
A dielectric material gets polarized when it placed in an electric field. The field produce due to the polarization of material minimize the effect of external field. Hence, the electric field inside a dielectric decreases when it is placed in an external electric field.
Q4. 10 J of work is done in moving a positive charge of 1 C between two points. What is the potential difference between these two points?
Solution
Potential difference = Work/charge = 10 J/ 1C = 10 V.
Q5. Write two important conclusions regarding the relation between electric field and electric potential.
Solution
Electric field is always in the direction in which rate of fall in potential is steepest (maximum).
Magnitude of electric field is given by the change in the magnitude of electric potential per unit displacement normal to the equipotential surface at the point.
Q6. What would be the work done if a point charge +q, is taken from a point P to the point Q on the circumference of a circle drawn with another point charge +q at the centre?
Solution
Work done is zero, because on the circumference, distance between two charges remains the same. Hence, VA = VB.
Q7. Find the total work done in charging the plates or energy stored in a capacitor.
Solution
The energy stored between the plates of a capacitor is the same as the work needed to build up the charges on the plates. As the charge on each plate increases, it becomes more and more difficult to add more charge. Hence every incremental charge addition on the plates would lead to higher and higher amounts of work done.
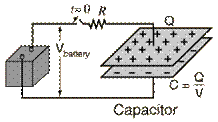 Now when a battery is connected to the capacitor and the circuit is closed, a current starts flowing. Then the capacitor slowly starts getting charged up. The voltage across the capacitor is proportional to the charge.
Therefore,V = q /C
As the charge builds, any increment in the charge dq would lead to work done by the battery in charging the capacitor plates. The total work done is given by the following integral.
Now when a battery is connected to the capacitor and the circuit is closed, a current starts flowing. Then the capacitor slowly starts getting charged up. The voltage across the capacitor is proportional to the charge.
Therefore,V = q /C
As the charge builds, any increment in the charge dq would lead to work done by the battery in charging the capacitor plates. The total work done is given by the following integral.
 Substituting, Q = CV, we can also write it as:
U = ½ CV2
Substituting, Q = CV, we can also write it as:
U = ½ CV2
 Now when a battery is connected to the capacitor and the circuit is closed, a current starts flowing. Then the capacitor slowly starts getting charged up. The voltage across the capacitor is proportional to the charge.
Therefore,V = q /C
As the charge builds, any increment in the charge dq would lead to work done by the battery in charging the capacitor plates. The total work done is given by the following integral.
Now when a battery is connected to the capacitor and the circuit is closed, a current starts flowing. Then the capacitor slowly starts getting charged up. The voltage across the capacitor is proportional to the charge.
Therefore,V = q /C
As the charge builds, any increment in the charge dq would lead to work done by the battery in charging the capacitor plates. The total work done is given by the following integral.
 Substituting, Q = CV, we can also write it as:
U = ½ CV2
Substituting, Q = CV, we can also write it as:
U = ½ CV2
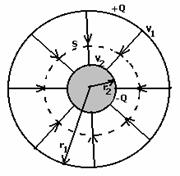
Q8. A spherical capacitor that consists of two concentric spherical conductors, held in position by suitable insulating supports. How can the capacitance of this arrangement be expressed in terms of its radii of outer and inner spheres r1 and r2?
Solution
A spherical capacitor consisting of two concentric spherical conductors, held in position by suitable insulating supports.
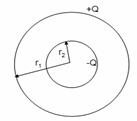 We know that the electric field between r1 and r2 is only due to charge –Q on the inner spherical shell.
The uniform charge on the outer sphere produces zero electric field inside the sphere.
So the net electric field at distance r from the centre is given with direction radially inward because it is due to negative charge,
We know that the electric field between r1 and r2 is only due to charge –Q on the inner spherical shell.
The uniform charge on the outer sphere produces zero electric field inside the sphere.
So the net electric field at distance r from the centre is given with direction radially inward because it is due to negative charge, 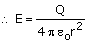
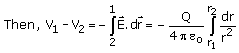
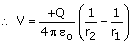 From the definition of capacitance,
From the definition of capacitance,
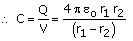
 We know that the electric field between r1 and r2 is only due to charge –Q on the inner spherical shell.
The uniform charge on the outer sphere produces zero electric field inside the sphere.
So the net electric field at distance r from the centre is given with direction radially inward because it is due to negative charge,
We know that the electric field between r1 and r2 is only due to charge –Q on the inner spherical shell.
The uniform charge on the outer sphere produces zero electric field inside the sphere.
So the net electric field at distance r from the centre is given with direction radially inward because it is due to negative charge, 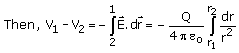

Q9. Why does the electric field inside a dielectric decrease, when it is placed in an external electric field?
Solution
When a dielectric is placed in an external electric field, it becomes polarized. The electric field due to polarization opposes the external electric field. Hence the electric field get reduce.
Q10. Two identical plane metallic surfaces A and B are kept parallel to each other in air, separated by distance of 10 cm,
A is given a positive potential of 10 V, and the other surface of B is earthed.
(1) What is the magnitude and direction of the uniform electric field between Y and Z? (2) What is the work done in moving a charge of 10 μC from X to Y?


Solution
(1) Potential difference between y and z is given as,
Since surface of B is earthed therefore potential at Z will be zero
Hence, V = VY - VZ = 10 - 0 = 10 V
The electric field between Y and Z is given as,
 The direction of the electric field is from plate A to plate B.
(2) Points X and Y are on same plate; hence, they are at the same potential
VX = VY = 10 V
Therefore, work done in moving a charge of 10 μC from X to Y
W = q0 × (VX - VY) = q0 × (10 -10) = 0
The direction of the electric field is from plate A to plate B.
(2) Points X and Y are on same plate; hence, they are at the same potential
VX = VY = 10 V
Therefore, work done in moving a charge of 10 μC from X to Y
W = q0 × (VX - VY) = q0 × (10 -10) = 0
 The direction of the electric field is from plate A to plate B.
(2) Points X and Y are on same plate; hence, they are at the same potential
VX = VY = 10 V
Therefore, work done in moving a charge of 10 μC from X to Y
W = q0 × (VX - VY) = q0 × (10 -10) = 0
The direction of the electric field is from plate A to plate B.
(2) Points X and Y are on same plate; hence, they are at the same potential
VX = VY = 10 V
Therefore, work done in moving a charge of 10 μC from X to Y
W = q0 × (VX - VY) = q0 × (10 -10) = 0
Q11. Explain the principle behind the operation of a Van de Graff generator.
Solution
Consider a large spherical conducting shell of radius R1 with uniform charge density and total charge q1.
The electric field inside the shell is zero. Since the electric field is zero, the inside of the spherical shell has ΔV = 0, i.e., it is an equipotential surface and the electric potential at any point inside the shell will be same everywhere and is equal to the potential at the surface
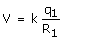 Now consider a small sphere of radius R2 carrying a uniform surface charge q2.
Now consider a small sphere of radius R2 carrying a uniform surface charge q2.
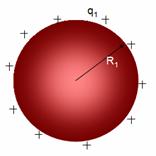
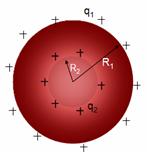 The electric field at any point at a distance r outside R2 due to the charge q2 is radially outwards from the centre and its magnitude is
The electric field at any point at a distance r outside R2 due to the charge q2 is radially outwards from the centre and its magnitude is  , so the electric field in the region between R1 and R2 is only due to charge q2 and is pointing radially outwards so the potential must be higher on smaller sphere than the larger sphere because the electric field lines always point from the region of higher potential to lower potential. Also a positive charge always feels force from higher to lower potential. So if we connect the two spheres, the positive charges will move from smaller sphere to the larger spherical shell. The smaller sphere remains at a higher potential compared to the larger sphere regardless of the charge on the two spheres.
If somehow we put some charge on the smaller sphere and then connect it with the larger sphere, the charge will continue to flow from inner to outer sphere and large amount of charge q1 can build up on the outer sphere. By accumulating a large amount of charge, the potential on the outer sphere can become very large of the order of millions of volts. This is the principle of Van de Graff generator.
, so the electric field in the region between R1 and R2 is only due to charge q2 and is pointing radially outwards so the potential must be higher on smaller sphere than the larger sphere because the electric field lines always point from the region of higher potential to lower potential. Also a positive charge always feels force from higher to lower potential. So if we connect the two spheres, the positive charges will move from smaller sphere to the larger spherical shell. The smaller sphere remains at a higher potential compared to the larger sphere regardless of the charge on the two spheres.
If somehow we put some charge on the smaller sphere and then connect it with the larger sphere, the charge will continue to flow from inner to outer sphere and large amount of charge q1 can build up on the outer sphere. By accumulating a large amount of charge, the potential on the outer sphere can become very large of the order of millions of volts. This is the principle of Van de Graff generator.

 The electric field at any point at a distance r outside R2 due to the charge q2 is radially outwards from the centre and its magnitude is
The electric field at any point at a distance r outside R2 due to the charge q2 is radially outwards from the centre and its magnitude is  , so the electric field in the region between R1 and R2 is only due to charge q2 and is pointing radially outwards so the potential must be higher on smaller sphere than the larger sphere because the electric field lines always point from the region of higher potential to lower potential. Also a positive charge always feels force from higher to lower potential. So if we connect the two spheres, the positive charges will move from smaller sphere to the larger spherical shell. The smaller sphere remains at a higher potential compared to the larger sphere regardless of the charge on the two spheres.
If somehow we put some charge on the smaller sphere and then connect it with the larger sphere, the charge will continue to flow from inner to outer sphere and large amount of charge q1 can build up on the outer sphere. By accumulating a large amount of charge, the potential on the outer sphere can become very large of the order of millions of volts. This is the principle of Van de Graff generator.
, so the electric field in the region between R1 and R2 is only due to charge q2 and is pointing radially outwards so the potential must be higher on smaller sphere than the larger sphere because the electric field lines always point from the region of higher potential to lower potential. Also a positive charge always feels force from higher to lower potential. So if we connect the two spheres, the positive charges will move from smaller sphere to the larger spherical shell. The smaller sphere remains at a higher potential compared to the larger sphere regardless of the charge on the two spheres.
If somehow we put some charge on the smaller sphere and then connect it with the larger sphere, the charge will continue to flow from inner to outer sphere and large amount of charge q1 can build up on the outer sphere. By accumulating a large amount of charge, the potential on the outer sphere can become very large of the order of millions of volts. This is the principle of Van de Graff generator.
Q12. An inflated balloon is charged by rubbing with fur. Will it stick readily to a conducting wall or to an insulating wall?
Solution
It will stick readily to the conducting wall. It induces an equal amount of charge on the conducting wall and a lesser charge on insulating wall. Thus, a large force of attraction acts between the balloon and the conducting wall.
Q13. Two positive point charges of 0.2 μC and 0.01 μC are placed 10 cm apart. Calculate the work done in reducing the distance to 5 cm.
Solution
Given:
q1 = 0.2 μC
q2 = 0.01 μC
r1 = 10 cm = 0.1 m
r2 = 5 cm = 0.05
Work done in reducing the distance from 10 cm to 5 cm can be calculate by using the relation




Q14. There are two capacitors of capacitance C1 and C2 connected in series. Calculate the equivalent capacitance of the system. 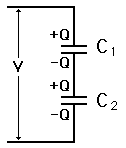
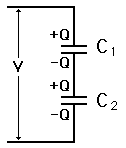
Solution
The capacitors in series are connected one after the other in a row, back to back.
In case of series capacitors, positive plate of one capacitor is attached to the negative plate of the successive capacitor.
The distribution of charges from the battery results in equal charges appearing on each one of the capacitors connected in series. Also note that the sum of the potential difference across each capacitor is equal to the total potential difference.
Therefore, V1+V2 = V, which can be written in terms of charge as
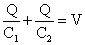 A single equivalent capacitance in series would imply
A single equivalent capacitance in series would imply
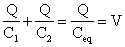 This further gives,
This further gives, 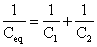
Q15. Explain the principle of a capacitor.
Solution
A capacitor has large electrical capacitance.
To understand the principle of a capacitor, consider an insulated metal plate A. Let some positive charge be given to this plate, till its potential becomes maximum.
Now bring another metallic plate B of same size near A. It is shown that equal amount of negative and positive charges are induced on plate B. Induced positive charge on B tends raise the potential on plate A ,but induced negative charge tends to lower the potential of A. However, if plate B is earthed then induced positive charge passes to earth. Hence the negative charge of B lowers the potential of A and consequently its capacitance is raised .It is the basic principle of a capacitor.


Q16. Points A, B, and C are situated at the circumference of a circle of radius r and a charge q is placed at its centre. A charge qo is brought from external point P away from the circle to A, B, C. In which case work done is maximum?
Solution
Potential at the points A, B, and C will be same as they lie on circumference of the circle. Hence the work done in bringing the charge qo from point P to any of the points A, B, and C will exactly same.
Q17. How much work has to be done to maintain electric dipole with moment 6 x 10-8 cm and angle 60o in an electric field of magnitude 1.2 x 104 N/C?
Solution
Given:
P = 6 x 10-8 cm
E = 1.2 x 104 N/C
θ = 60o
Work done = potential energy of dipole
= pE (cos 60o)
= -6 x 10-8 x 1.2 x 104 x 0.5
W = 3.6 x 10-4 J
Q18. How much work is required to be done to separate the charges of a dipole till infinity with Q ± 7μC and r = 0.18 m?
Solution
Given:
Q = ± 7μC
r = 0.18 m
Energy to be stored in the dipole, U = -K  U = -
U = -  = - 2.455 J
Therefor, 2.455 J work has to be done to separate the charges till infinity. The negative sign indicates that the work has to be done against the attraction of charges.
= - 2.455 J
Therefor, 2.455 J work has to be done to separate the charges till infinity. The negative sign indicates that the work has to be done against the attraction of charges.
 U = -
U = -  = - 2.455 J
Therefor, 2.455 J work has to be done to separate the charges till infinity. The negative sign indicates that the work has to be done against the attraction of charges.
= - 2.455 J
Therefor, 2.455 J work has to be done to separate the charges till infinity. The negative sign indicates that the work has to be done against the attraction of charges.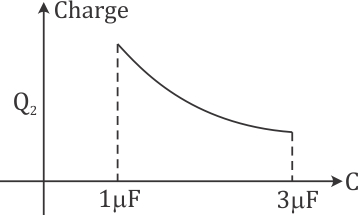
Comments
Post a Comment