Q1. Which combination of cells is the best to get maximum current, when the external resistance is much higher than the total internal resistance?
Solution
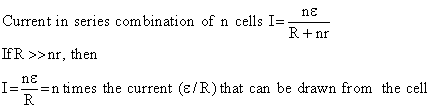 If the external resistance is much higher than the total internal resistance, then the cell should be connected in series to get maximum current.
If the external resistance is much higher than the total internal resistance, then the cell should be connected in series to get maximum current.
Q2. A conducting wire is stretched to increase its length by 2%. What is the percentage change in resistance?
Solution

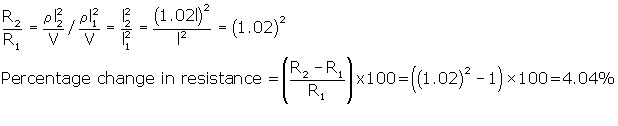
Q3. Name two substances whose resistivity decreases with the rise in temperature.
Solution
Resistivity of semiconductors decreases with rise in temperature. So, the two substances whose resistivity decreases with the rise in temperature are Silicon and Germanium.
Q4. Find the resistance between a and b in the circuit given below:
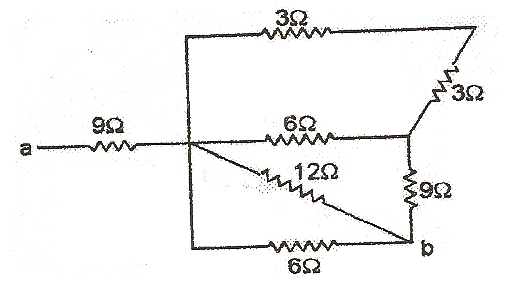
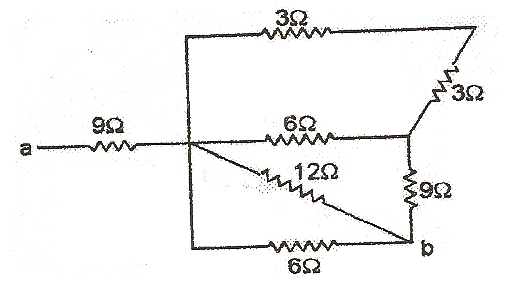
Solution
Here 3 Ω resistances are connected in series which are parallel to 6 Ω resistance.
 This 3 Ω resistance in series with 9 Ω this combination is in parallel to 12 Ω resistance.
This 3 Ω resistance in series with 9 Ω this combination is in parallel to 12 Ω resistance.
 This 6 Ω resistance is in parallel with 6 Ω, this whole combination is in series with 9 Ω resistance.
This 6 Ω resistance is in parallel with 6 Ω, this whole combination is in series with 9 Ω resistance.

 This 3 Ω resistance in series with 9 Ω this combination is in parallel to 12 Ω resistance.
This 3 Ω resistance in series with 9 Ω this combination is in parallel to 12 Ω resistance.
 This 6 Ω resistance is in parallel with 6 Ω, this whole combination is in series with 9 Ω resistance.
This 6 Ω resistance is in parallel with 6 Ω, this whole combination is in series with 9 Ω resistance.

Q5. What is the resistance across A and B in the figure?
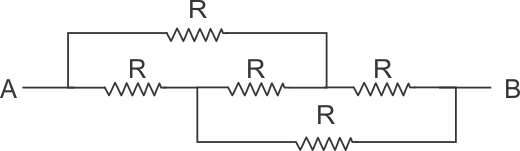

Solution
The equivalent circuit is shown in the figure. Since the bridge is balanced hence the resistance in the part KL is not in operation.
Hence, 2R and 2R are in parallel.


Q6. A wire has a resistance of 6 ohms. It is bent in the form of an equilateral triangle. The effective resistance between any two corners of the triangle is
Solution
By bending the wire into the form of an equilateral triangle is same as breaking the wire into 1/3rd and joining as an equilateral triangle. Hence, resistance of each side is (6/3) Ω , 2 Ω. In this triangle two sides are in series and the resultant parallel to the third side.
Therefore, for the total resistance R,
 ,
or R=4 /3 Ω
,
or R=4 /3 Ω
Q7. Three equal resistors each of resistance r are connected to form a triangle. The equivalent resistance across any two corners of the triangle is
Solution
In triangle circuit two sides are in series and are parallel to third side. Hence, its equivalent resistance will be:
.gif)
Q8. Mobility of charge carriers in a conductor is given by
Solution
Mobility of charge carriers in a conductor is given by drift velocity/ electric field
Q9. The internal resistance of a cell of emf 2 V is 0.1 ohm. It is connected to a resistance of 3.9 ohm. The voltage across cell will be (in volts)
Solution

Q10. Figure below shows an unbalanced Wheatstone bridge. What is the direction of conventional current between B and D?
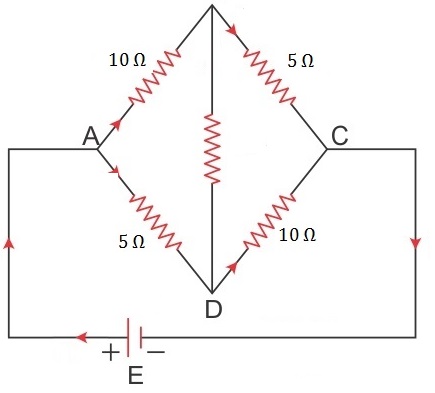

Solution
The potential drop across AD is less than that across AB. So, the potential of D is higher than that of B. Hence, the flow is from D to B.
Q11. What is the ratio of resistances of two conductors of same material having length l and 2l and radius r and r/2 respectively?
Solution
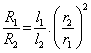
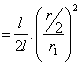
Q12. Meter Bridge or Slide Wire Bridge is a practical form of
Solution
Meter Bridge or Slide Wire Bridge is a practical form of Wheatstone bridge.
Q13. Five resistances are connected as shown in fig. The effective resistance between points A and B is 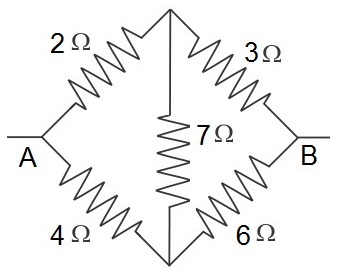

Solution
It is an example of a Wheatstone bridge with 2, 3 ohms in series connected parallel to 4 and 6 ohms. The resistors form a balanced condition and hence there is no current through the 7 Ω resistor.
Therefore the resultant resistance (R) is given by:
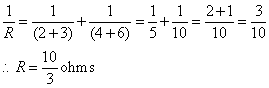
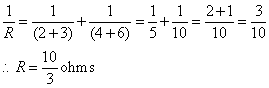
Q14. A car battery has _______resistance than a dry cell.
Solution
A car battery of 12 V provides a current of about 200 A, which is the current needed to operate a starter motor. So a battery has a very small internal resistance.
Q15. N resistors each of resistance R are first combined to get minimum possible resistance and then combined to get maximum possible resistance. The ratio of the minimum to maximum resistance is
Solution
The maximum resistance is NR and the minimum resistance is R/N, so their ratio is 1/N2
Q16. What is the total resistance of the circuit shown in the figure.
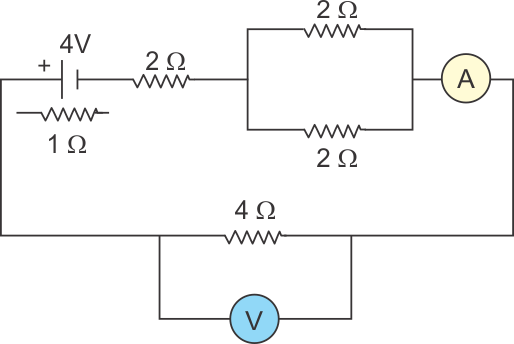

Solution
2 Ω and 2 Ω resistors are in parallel. So, its equivalent resistance is 1 Ω
Thus, the total resistance is = 2 Ω + 1 Ω + 4 Ω + 1 Ω = 8 Ω
Q17. What is the equivalent resistance across A and B in the figure if R = 3Ω?
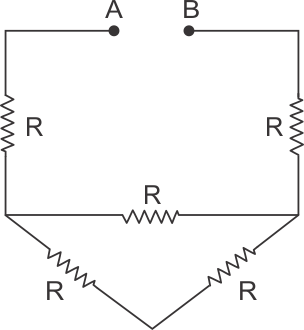

Solution
2R and R in parallel and then the resultant in series with R and R.
Thus, total resistance is


Q18. What do you mean by sensitivity of potentiometer? How can we increase the sensitivity of potentiometer?
Solution
A potentiometer is sensitive if it is capable of measuring the small potential differences and it shows significant change in balancing length for a small change in the potential difference being measured.
Sensitivity of potentiometer means the smallest potential difference that can be measured by using it and this can be achieved by decreasing the potential gradient by increasing the length of the wire or reducing the current in the potentiometer using rheostat.
Q19. When the position of cell and galvanometer in a Wheatstone bridge is inter-changed, its balanced condition
Solution
When the position of cell and galvanometer in a Wheatstone bridge is interchanged, the balanced condition remains unchanged.
Q20. Three resistors of 4 Ω, 12 Ω, and 6 Ω are connected in parallel. No. of 12 Ω resistors required to be connected in parallel to reduce the total resistance to half of its original is
Solution
The total resistance of 4 Ω, 12 Ω, and 6 Ω in parallel is 2 Ω. Suppose n is the number of 12-ohms resistor required to be connected to reduce the total resistance to half the original value, i.e. R’=2/2 = 1 Ω. The total resistance of n 12- ohms resistors in parallel is 12/n.


Q21. If there are n cells of emf E1, E2, …En and of internal resistances r1, r2, …rn , connected in parallel, the combination is equivalent to a cell of emf Eeq such that
Solution
If there are n cells of emf E1, E2, …En and of internal resistances r1, r2, …rn , connected in parallel, the combination is equivalent to a cell of emf Eeq such that
.gif)
.gif)
Q22. A carbon resistor is marked in green, red, and orange bands. The approximate resistance of the resistor is
Solution
Resistor colour code of green is 5, and that of red is 2. The first two numbers indicate significant figures of the resistance in ohm. The third band indicates the decimal multiplier. So, the total resistance of the given problem is 52 × 10³ Ω.
Q23. Find the current in the circuit shown in the figure below 


Solution
The resistances in the branch BC and AC are connected in series.


Q24. What is the maximum current that can be drawn from a cell of emf E and internal resistance r connected to an external resistance R?
Solution
As the maximum current that can be drawn from a cell is for R =0 and it is I = E/r.
Q25. Out of two bulbs marked 25 W and 100 W, which has higher resistance?
Solution
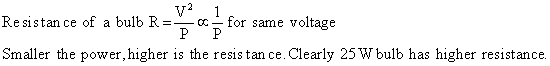
Q26. In the following circuit the potential difference between points X and Y is
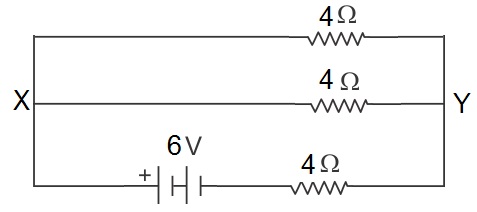

Solution
The current flowing out of battery is 6 / (2+4) = 1 A. Voltage drop across 4 ohm resistance is 4 V. The potential difference, i. e.,
6- 4 = 2 will appear between X and Y terminals.
Q27. The resistance across the legs M and N of the letter A as shown in the following figure is :


Solution
In given circuit two 4 Ω resistances are in series and parallel with the resistance 4 Ω which are connected to the two 4 Ω resistance in series. Hence, resistance across the M and N will be,
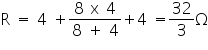
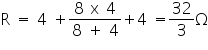
Q28. The current in 2 ohm resistor shown in the figure below is 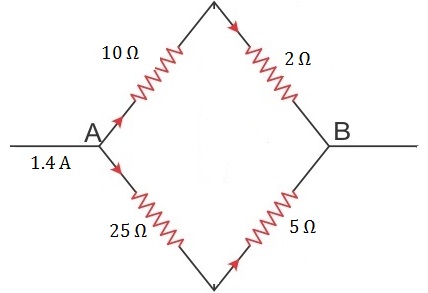

Solution
Current in 2 ohm resistor = 

Q29. The SI unit for measuring internal resistance is
Solution
The SI unit for measuring internal resistance is ohm
Q30. Two identical cells are connected in series and then in parallel. When connected it series they send a current of 10 A through a 5 Ω resistor and when connected in parallel they send a current of 8 A. What is the internal resistance of each cell?
Solution

Q31. Two wires of equal lengths, one of copper and other nickel have the same resistance. Which wire is thicker?
Solution
Let  and
and  be resistivities of copper and nickel. A1 and A2 be the area of cross-section these wires. Since the two wires have the equal lengths and have the same resistance, therefore:
be resistivities of copper and nickel. A1 and A2 be the area of cross-section these wires. Since the two wires have the equal lengths and have the same resistance, therefore:
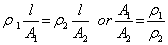 Since the resistivity of copper
Since the resistivity of copper  is less than that of nickel (
is less than that of nickel ( ), it follows that area of cross-section of copper wire is less than that of nickel wire. Thus, nickel wire is thicker.
), it follows that area of cross-section of copper wire is less than that of nickel wire. Thus, nickel wire is thicker.
Q32.
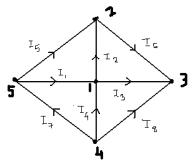 In the given network find the value of
In the given network find the value of  if the values of current I1 = 1 A, I2 = 2 A, I3 = 4 A, I8 = 5 A
if the values of current I1 = 1 A, I2 = 2 A, I3 = 4 A, I8 = 5 A
 In the given network find the value of
In the given network find the value of  if the values of current I1 = 1 A, I2 = 2 A, I3 = 4 A, I8 = 5 A
if the values of current I1 = 1 A, I2 = 2 A, I3 = 4 A, I8 = 5 ASolution

Q33. The term open circuit means
Solution
The term open circuit means no current flows through the cell.
Q34. In the figure, what will be the reading of the ammeter and voltmeter, when the key K is closed? The internal resistance of the cell is zero.
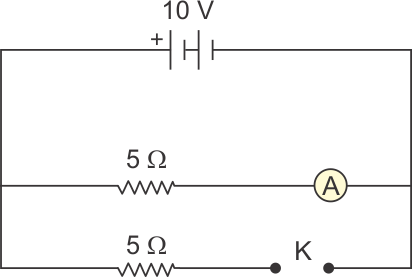

Solution
Voltmeter is in parallel with the cell. And total resistance in the circuit is 2.5 Ω.
Q35. What will be the resistivity of a wire if it is stretched to double of its original length without loss of mass?
Solution
The resistivity of a wire depends on the nature of material but not on its dimensions. Thus, the increase in length of the wire will not affect its resistivity.
Q36. In the figure a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null point for the two primary cells of emfs  and
and  connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i)
connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i)  /
/  and (ii) position of null point for the cell
and (ii) position of null point for the cell  . How is the sensitivity of a potentiometer increased?
. How is the sensitivity of a potentiometer increased?
 OR
Using Kirchoff's rules determine the value of unknown resistance R is the circuit so that no current flows through 4 Ω resistance. Also find the potential difference between A and D.
OR
Using Kirchoff's rules determine the value of unknown resistance R is the circuit so that no current flows through 4 Ω resistance. Also find the potential difference between A and D.
 and
and  connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i)
connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i)  /
/  and (ii) position of null point for the cell
and (ii) position of null point for the cell  . How is the sensitivity of a potentiometer increased?
. How is the sensitivity of a potentiometer increased?
Solution
As v  L in potentiometer,
L in potentiometer,




 (i)
(i)  (ii) E1 - E2=120 × K
E1 - 3/7E1=120 K
E1 = 210 K
SO L or E1 = 210cm
by increasing the length of the wire ints rensititis can be increases.
OR
as I (1 + 1 + R) = 1 - 3
(ii) E1 - E2=120 × K
E1 - 3/7E1=120 K
E1 = 210 K
SO L or E1 = 210cm
by increasing the length of the wire ints rensititis can be increases.
OR
as I (1 + 1 + R) = 1 - 3
 I =
I =  .....(1)
Now in loop I, 9 - 6 = 2I
3 = 2I
.....(1)
Now in loop I, 9 - 6 = 2I
3 = 2I
 I =
I =  A
Put it in (1)
A
Put it in (1)  R = 2 Ω
R = 2 Ω
 L in potentiometer,
L in potentiometer,




 (i)
(i)  (ii) E1 - E2=120 × K
E1 - 3/7E1=120 K
E1 = 210 K
SO L or E1 = 210cm
by increasing the length of the wire ints rensititis can be increases.
OR
as I (1 + 1 + R) = 1 - 3
(ii) E1 - E2=120 × K
E1 - 3/7E1=120 K
E1 = 210 K
SO L or E1 = 210cm
by increasing the length of the wire ints rensititis can be increases.
OR
as I (1 + 1 + R) = 1 - 3
 I =
I =  .....(1)
Now in loop I, 9 - 6 = 2I
3 = 2I
.....(1)
Now in loop I, 9 - 6 = 2I
3 = 2I
 I =
I =  A
Put it in (1)
A
Put it in (1)  R = 2 Ω
R = 2 Ω
Q37. If the temperature of a conductor increases, how does the relaxation time of electrons in the conductor changes?
Solution
When the temperature of the conductor increases, the resistivity of the conductor increases and hence according to the formula 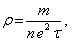 the relaxation period
the relaxation period  decreases.
decreases.
Q38. Calculate the electrical conductivity of the material of a conductor of length 2 m, area of cross-section 0.02 mm2 having a resistance of 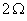
Solution
R = 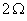 , A = 0.02 mm2 = 0.02 x 10-6 m2 = 2 x 10-8 m2, l = 2 m
Using the relation,
, A = 0.02 mm2 = 0.02 x 10-6 m2 = 2 x 10-8 m2, l = 2 m
Using the relation,
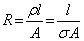 Electrical conductivity
Electrical conductivity
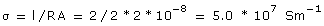
Q39.  In a given circuit diagram
In a given circuit diagram  = 2.0 V.
= 2.0 V.  = 6.0 V respectively and resistance r1, r2 and R are 2.0 W, 4.0 W and 10.0 W respectively. Calculate the value of current and indicate its direction.
Also calculate the potential difference between the points
(i) B and A
(ii) A and C.
= 6.0 V respectively and resistance r1, r2 and R are 2.0 W, 4.0 W and 10.0 W respectively. Calculate the value of current and indicate its direction.
Also calculate the potential difference between the points
(i) B and A
(ii) A and C.
 = 2.0 V.
= 2.0 V.  = 6.0 V respectively and resistance r1, r2 and R are 2.0 W, 4.0 W and 10.0 W respectively. Calculate the value of current and indicate its direction.
Also calculate the potential difference between the points
(i) B and A
(ii) A and C.
= 6.0 V respectively and resistance r1, r2 and R are 2.0 W, 4.0 W and 10.0 W respectively. Calculate the value of current and indicate its direction.
Also calculate the potential difference between the points
(i) B and A
(ii) A and C.Solution
In the given circuit the cells are connected in series, but their positive terminals are connected together, so they oppose each other.
 = 2.0 V,
= 2.0 V,  = 6.0 V, r1 = 2.0 Ω, r2 = 4.0 Ω, R = 10.0 Ω
Therefore, Net emf =
= 6.0 V, r1 = 2.0 Ω, r2 = 4.0 Ω, R = 10.0 Ω
Therefore, Net emf =  -
-  = 6.0 - 2.0 = 4.0 V
Net internal resistance rint = r1 + r2 = 2.0 + 4.0 = 6.0 Ω
Therefore, Current in circuit, I =
= 6.0 - 2.0 = 4.0 V
Net internal resistance rint = r1 + r2 = 2.0 + 4.0 = 6.0 Ω
Therefore, Current in circuit, I =  As
As  ,the direction of current in circuit is along B and C anticlockwise. The current in circuit is along conventional direction of cell
,the direction of current in circuit is along B and C anticlockwise. The current in circuit is along conventional direction of cell  , but opposite to conventional direction of cell
, but opposite to conventional direction of cell  , therefore
(i) p. d across B and A
VA-VB =
, therefore
(i) p. d across B and A
VA-VB =  - Ir2 = 6.0 - 0.25 x 4.0 = 5.0 V
(ii) p.d across A and C,
VA - VC =
- Ir2 = 6.0 - 0.25 x 4.0 = 5.0 V
(ii) p.d across A and C,
VA - VC =  + I r1 = 2.0 + 0.25 x 2.5 V = 2.625 V
+ I r1 = 2.0 + 0.25 x 2.5 V = 2.625 V
 = 2.0 V,
= 2.0 V,  = 6.0 V, r1 = 2.0 Ω, r2 = 4.0 Ω, R = 10.0 Ω
Therefore, Net emf =
= 6.0 V, r1 = 2.0 Ω, r2 = 4.0 Ω, R = 10.0 Ω
Therefore, Net emf =  -
-  = 6.0 - 2.0 = 4.0 V
Net internal resistance rint = r1 + r2 = 2.0 + 4.0 = 6.0 Ω
Therefore, Current in circuit, I =
= 6.0 - 2.0 = 4.0 V
Net internal resistance rint = r1 + r2 = 2.0 + 4.0 = 6.0 Ω
Therefore, Current in circuit, I =  As
As  ,the direction of current in circuit is along B and C anticlockwise. The current in circuit is along conventional direction of cell
,the direction of current in circuit is along B and C anticlockwise. The current in circuit is along conventional direction of cell  , but opposite to conventional direction of cell
, but opposite to conventional direction of cell  , therefore
(i) p. d across B and A
VA-VB =
, therefore
(i) p. d across B and A
VA-VB =  - Ir2 = 6.0 - 0.25 x 4.0 = 5.0 V
(ii) p.d across A and C,
VA - VC =
- Ir2 = 6.0 - 0.25 x 4.0 = 5.0 V
(ii) p.d across A and C,
VA - VC =  + I r1 = 2.0 + 0.25 x 2.5 V = 2.625 V
+ I r1 = 2.0 + 0.25 x 2.5 V = 2.625 V
Q40. Find the resistance across A and B in the circuit given below:

Solution
The given circuit is balanced Wheatstone bridge. Therefore, zero resistance between ec.
The balanced bridge is given below:
 Equivalent circuit is:
Equivalent circuit is:
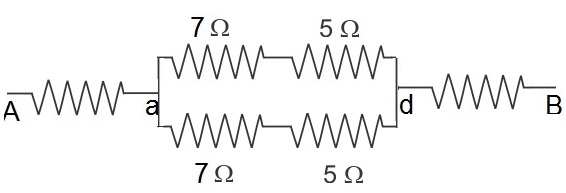

 Equivalent circuit is:
Equivalent circuit is:


Q41. Two bulbs one of 50 watt and another of 25 watt are connected in series to the mains. Find the ratio of the currents through them.
Solution
As the bulbs are in series the same current flows through each of them.
Q42. What is the purpose of using a resistance in series during charging a circuit?
Solution
During the charging of a battery, current will flow in a direction opposite to the direction of current drawn from a battery. Purpose of having a series resistance in charging circuit is to adjust the charging current.
Q43. What is Kirchhoff's second law or Kirchhoff's loop law or Kirchhoff's voltage law?


Solution
According to the Kirchhoff's voltage law,
In any closed path of an electrical circuit (or closed loop), the algebraic sum of all the potential differences is zero i.e


Q44. A cell of emf 8 V and internal resistance of 0.5 ohm is connected across a load of resistance (i) 15.5 ohm (ii) 11.5 ohm. Calculate the potential drop in each case.
Solution
(i) When the load resistance is 15.5 ohm
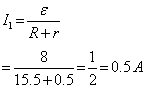 V1 = E - I1rV1 = 8 - (0.5 × 0.5)V1 = 7.75 V
(ii) When the load resistance is 11.5 ohm
V1 = E - I1rV1 = 8 - (0.5 × 0.5)V1 = 7.75 V
(ii) When the load resistance is 11.5 ohm
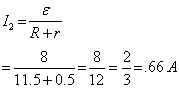 V2 = E - I2r
V2 = 8 - (0.66 × 0.5)
V2 = 7.67 V
V2 = E - I2r
V2 = 8 - (0.66 × 0.5)
V2 = 7.67 V
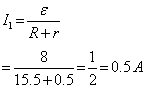 V1 = E - I1rV1 = 8 - (0.5 × 0.5)V1 = 7.75 V
(ii) When the load resistance is 11.5 ohm
V1 = E - I1rV1 = 8 - (0.5 × 0.5)V1 = 7.75 V
(ii) When the load resistance is 11.5 ohm
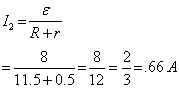 V2 = E - I2r
V2 = 8 - (0.66 × 0.5)
V2 = 7.67 V
V2 = E - I2r
V2 = 8 - (0.66 × 0.5)
V2 = 7.67 V
Q45. What is mobility of electrons and how is it related with the conductivity?
Solution
Mobility of electrons in a conductor is defined as the magnitude of the drift velocity per unit electric field.
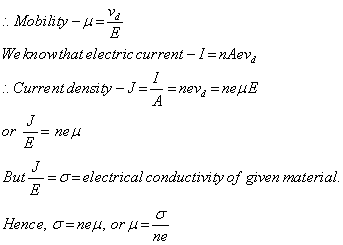
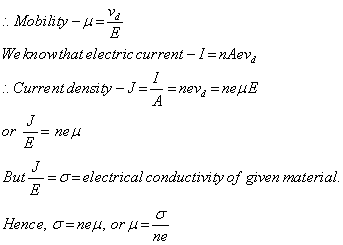
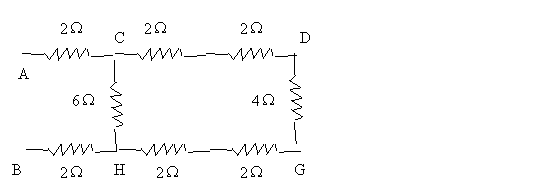
Q46. Determine the equivalent resistance between terminals A and B of network shown in the figure below:


Solution
Two 2-ohm resistors at the extreme right are sufficient in determining the equivalent resistance and may be assumed as absent. The resistance in branch DEFG are in series (= 2+2+4+2+2= 12 ) and this branch is in parallel with the branch DG (= 6
) and this branch is in parallel with the branch DG (= 6 )
)
 Resistance between D and G , RDG=
Resistance between D and G , RDG=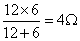 The circuit shown in the figure above reduces to the figure below:
The circuit shown in the figure above reduces to the figure below:
 Resistance between C and H, RCH=
Resistance between C and H, RCH=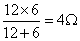 The circuit then further reduces to the figure below:
The circuit then further reduces to the figure below: RAB = 2+2+4 = 8
RAB = 2+2+4 = 8
 Resistance between C and H, RCH=
Resistance between C and H, RCH= RAB = 2+2+4 = 8
RAB = 2+2+4 = 8
Q47. A conductor of length l is connected to battery of potential V. If the length of the conductor is tripled by stretching it, keeping V constant, explain how the following factors vary in the conductor. (i) Drift velocity of electrons (ii) Resistivity
Solution
(i) 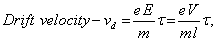 , hence on increasing the length three times, the drift velocity becomes one-third of its original value.
(ii) Resistivity
, hence on increasing the length three times, the drift velocity becomes one-third of its original value.
(ii) Resistivity 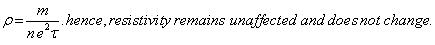
Q48. The following graph shows the variation of terminal potential difference V, across a combination of three cells in series to a resistor, versus current I :
 (i) calculate the emf of each cell.
(ii) for what current I, will th power dissipation of the circuit be maximum ?
(i) calculate the emf of each cell.
(ii) for what current I, will th power dissipation of the circuit be maximum ?
 (i) calculate the emf of each cell.
(ii) for what current I, will th power dissipation of the circuit be maximum ?
(i) calculate the emf of each cell.
(ii) for what current I, will th power dissipation of the circuit be maximum ?Solution

Q49. Two wires A and B are of same material, have same area of cross-section and have their length in the ration 2: 1. What will be the ratio of current flowing through them if the same potential is applied across the length of each of them?
Solution
Current –
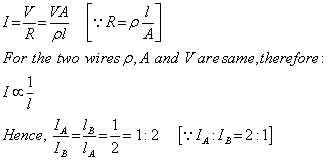
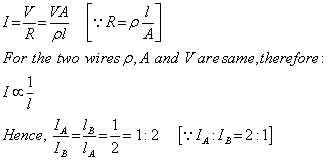
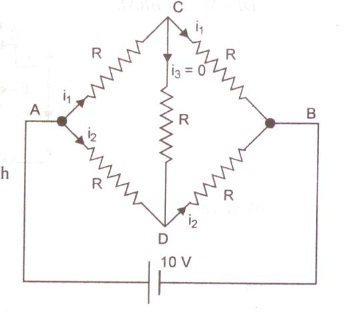
Q50. (i) Calculate the equivalent resistance of the given electrical network between points A and B.
(ii) Also calculate the current through CD and ACB if a 10 V dc source is connected between points A and B and the value of R 2 Ω.


Solution
(i) The equivalent circuit is shown in fig. It is balanced wheatstone bridge. So, the resistance connected between C and D is ineffective.
 Resistance of arm ACB, R1 = R + R = 2R
Resistance of arm ADB, R2 = R + R = 2R
Equivalent resistance between A and B, RAB is given by
Resistance of arm ACB, R1 = R + R = 2R
Resistance of arm ADB, R2 = R + R = 2R
Equivalent resistance between A and B, RAB is given by
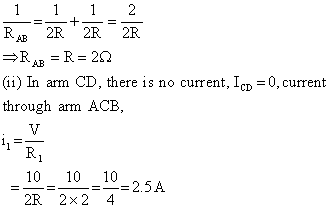
 Resistance of arm ACB, R1 = R + R = 2R
Resistance of arm ADB, R2 = R + R = 2R
Equivalent resistance between A and B, RAB is given by
Resistance of arm ACB, R1 = R + R = 2R
Resistance of arm ADB, R2 = R + R = 2R
Equivalent resistance between A and B, RAB is given by
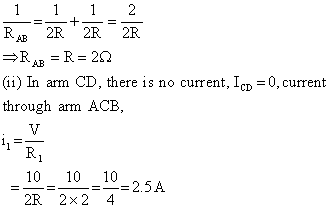
Q51. You are given three bulbs of 25, 40 and 60 W. Which of them has the lowest resistance?
Solution
 so the bulb with the highest power has the lowest resistance.
so the bulb with the highest power has the lowest resistance.
Q52. Show graphically the variation of resistivity with temperature for (i) Nichrome, (ii) carbon and (iii) semiconductors.
Solution
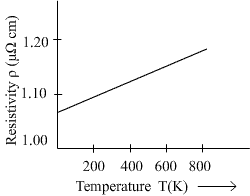
Resistivity of Nichrome as a function of absolute temperature T.
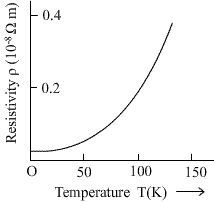
 (ii) Resistivity of carbon as a function of temperature T.
(ii) Resistivity of carbon as a function of temperature T.
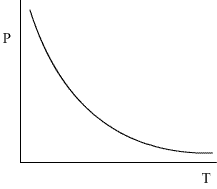
 (iii) Temperature dependence of resistivity for a semiconductor
(iii) Temperature dependence of resistivity for a semiconductor
 (ii) Resistivity of carbon as a function of temperature T.
(ii) Resistivity of carbon as a function of temperature T.
 (iii) Temperature dependence of resistivity for a semiconductor
(iii) Temperature dependence of resistivity for a semiconductor

Q53. A potentiometer wire is 5 m long and a potential difference of 6 V is maintained between its ends. Find the emf of a cell which balances against a length of 180 cm of the potentiometer wire.
Solution
Potential gradient of the potentiometer wire is:


Q54. The potential difference across a cell is 2 V when a current of 1 A is drawn from it. The potential difference falls to 1.8 V when a current of 1.2 A is drawn. Find the emf and internal resistance of the cell.
Solution
Using the relation:
V = E - I r
2 = E - 1 r ...............(1)
1.8 = E - 1.2 r ...............(2)
Subtracting (2) from (1) we get,
0.2 = 0.2 r
r = 1 Ω
From (1),
2 = E - (1 × 1) = E - 1
E = (2+1) V = 3 V
Q55. What is the equivalent resistance between the terminals A and B in the figure below:


Solution
The network shown in the above figure can be redrawn as shown in the figure below.
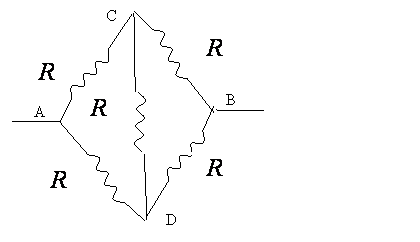 It is a balanced wheatstone bridge. Therefore, point C and D are at the same potential. Since no current flows in the branch CD, this branch is ineffective in determining the equivalent resistance between terminal A and B and can be removed. The branch ABC (= R+R= 2R) is in parallel with the branch ADB (= R+R= 2R)
It is a balanced wheatstone bridge. Therefore, point C and D are at the same potential. Since no current flows in the branch CD, this branch is ineffective in determining the equivalent resistance between terminal A and B and can be removed. The branch ABC (= R+R= 2R) is in parallel with the branch ADB (= R+R= 2R)
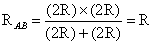
 It is a balanced wheatstone bridge. Therefore, point C and D are at the same potential. Since no current flows in the branch CD, this branch is ineffective in determining the equivalent resistance between terminal A and B and can be removed. The branch ABC (= R+R= 2R) is in parallel with the branch ADB (= R+R= 2R)
It is a balanced wheatstone bridge. Therefore, point C and D are at the same potential. Since no current flows in the branch CD, this branch is ineffective in determining the equivalent resistance between terminal A and B and can be removed. The branch ABC (= R+R= 2R) is in parallel with the branch ADB (= R+R= 2R)
Q56. Large amount of current can be obtained from the small drift velocity and small electronic charge in a conductor. Why?
Solution
Magnitude of current depends upon the electron density. The density of electrons per unit area is so enormous, that a small drift in electrons produce a large amount of current in a conductor.
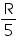
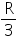
.gif)
Comments
Post a Comment